Hi there, I’m Marie. I spend time at the frontier of AI and software engineering for a living. If you don’t mind my chaotic publication schedule, don’t hesitate to…
Now, the biggest event of the summer isset to begin tomorrow, July 10, 2025. The best reasoning AI systems will have a chance to be put to the test, not in Silicon Valley… but on the Sunshine Coast of Australia.
A place more famous for humpback whales and beach towels than for mathematical prowess, but the place chosen to host the International Mathematical Olympiad (IMO) in July 2025.
What a fitting place to spend 3 days stuck in a classroom solving hardcore math problems - credit @Mooloolaba on flickr
Funny how things go. It is the second time ever that Australia has hosted the prestigious IMO, with the first being Canberra in 1988. However, that last Australian competition was a bit of a “wow” landmark moment for human intelligence when 13-year-old Australian mathematician (yes, 13) Terrence Tao became the youngest-ever gold medalist. Tao is now recognized as one of the world's most brilliant mathematicians and will return to this year’s edition to deliver a special guest lecture to participating students.
However, this is not a typical IMO. Moving in the shadows, AI research teams are working separately on systems capable of tackling the same unseen IMO problems that human contestants will face. There is no formal AI competition structure between humans and AIs. Each AI team looking to move the SOTA forward has to gain access to the official problems and publish their results independently, creating a fascinating natural experiment in AI reasoning capabilities.
The Challenge
What makes the IMO particularly interesting is its imprevisible, organic nature.
The IMO wasn't designed as an AI challenge, but its format—presenting never-before-seen problems requiring creative insight rather than memorization—inadvertently creates the perfect proving ground for genuine machine reasoning (if you read my previous posts you’ll know how much I liked ARC-AGI for the same reason *before OpenAI spent millions to brute force it).
On the AI side, each team brings distinctly different philosophical and technical approaches to the problem of mathematical reasoning. The stakes extend far beyond mathematical problem-solving: Deepmind’s Alphaproof first silver medal in 2024 lit a beacon in every AI researcher’s heart, and the best of the industry have spent time and compute tackling this challenge.
Depending on the outcome, these IMOs will give us a hint of where we stand. Whether our current machines can mimic our "thinking" in domains requiring creative insight rather than pattern recognition, or whether even with (almost) infinite compute data and resources, AI is still defeated by “very hard high school maths”.
Why it matters: Finally, a hard, unpoisoned benchmark For decades, the International Mathematical Olympiad (IMO) has represented the pinnacle of mathematical problem-solving for young humans.
Unlike standardized tests or games with fixed rules, the IMO demands creative problem-solving that stretches beyond pattern recognition: each year's problems are deliberately crafted to be novel, requiring contestants to develop unique insights rather than applying memorized techniques.
This environment creates a perfect testing ground for AI reasoning capabilities, mainly because:
Problems require multi-step logical reasoning.
Solutions demand creative insights that can't be derived through brute-force computation.
Questions are intentionally designed to avoid similarity to past problems, preventing both humans and AI from "training" on historical examples.
The IMO wasn’t designed for AI, and that’s the whole point.
It presents six math problems across two days that are novel, require multi-step reasoning, and are, as it happens, hard to formalize. It’s not a test you can “train on”. And because it's not an AI-specific benchmark, there's no reward for being overfitted. That alone makes it more honest than 95% of published evals right now.
Based on my discussions with some of the teams (*cough* - all the non-Chinese teams are full of fellow French people) fit to attempt the challenge, the difficulty varies significantly across mathematical domains with geometry being quite “solved” to Combinatorics presenting the harder challenge.
If your prépa 🇫🇷 or university days are far in the past, let me refresh your memory on what these different categories are with a few examples of IMO problems :
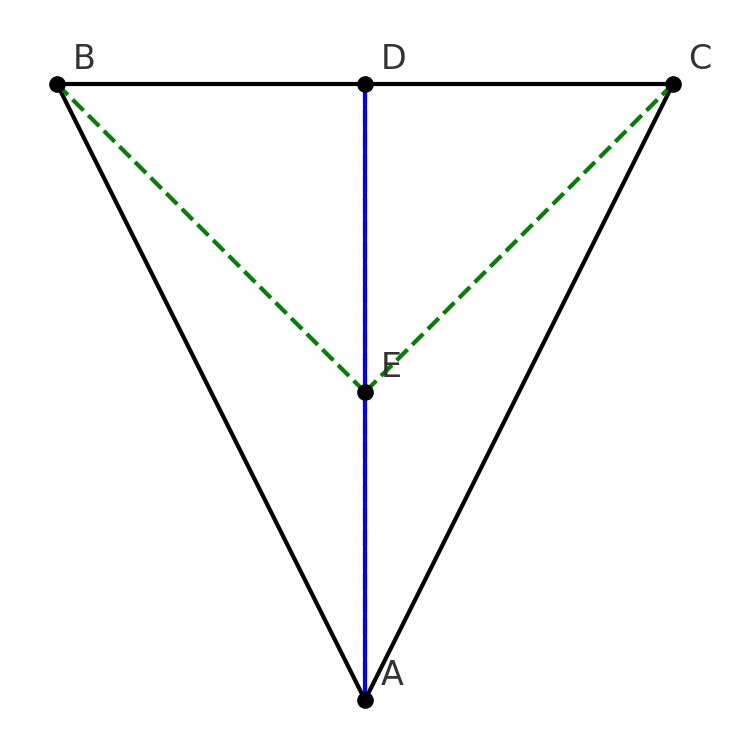
Geometry (from IMO 2011): Let ABC be a triangle with AB=AC. The angle bisector of ∠BAC meets BC at D. A point E lies on the segment AD such that AE=ED. Prove that BE=EC.
Number theory (from IMO 2015): Prove that for each positive integer n, there exist n consecutive positive integers, none of which is an integral power of a prime For example: for n=5, “90, 91, 92, 93, 94” works because 90 = 2 × 3 × 3 × 5, 91 = 7 × 13, 92 = 2 × 2 × 23, 93 = 3 × 31, 94 = 2 × 47 → none of them is a single prime exponent.
Combinatorics (from IMO 2014): In a tournament with 2n+1 players (no ties), each pair plays once. Show that there’s a player who, for every other player, either beats them or beats someone who beats them.
If you care, this proof actually has a name, it’s called the King’s Lemma (there is always a “dominant” player in a tournament with an odd number of players). To make it more “visual” I had chatgpt generate all possible tournament outcomes with n=3.
There is always a dominant player.
On a scale of 0 to 10, how hard is it, though? The last combinatorics problem was solved by roughly 15% of the 2014 IMO contestants (143 high-school students) that year.
To solve IMO problems reliably, especially Q4–Q6 (the harder problems), the participants are likely (1) in the top 0.001% cognitive ability range of their age, which corresponds roughly to an IQ > 145, (2) to have received special IMO training, and (3) to be showing a uniquely strong drive for a kid aged 14-18yo.
note: this chart is a log scale and intellectually, not absolutely sound, but gives you a good idea of the human population the AI systems are competing against
However, they are still a million miles away from a very hard challenge like the Millenium Prize problems (still unsolved by humans).
To solve IMO problems, the proof is usually short, <50 lines long which makes this accessible to current AI models who don’t do well on long form. You would need to be extremely smart, but the tools at your disposal are all “clear”, you would not need to be knowledgeable in multiple advanced math fields or don’t have to invent entirely new mathematical paradigms.
How should AI be evaluated?
The IMOs eliminate the criticism often leveled at AI benchmarks that they represent "teaching to the test." Here, neither humans nor machines can optimize for specific problem formats since the IMO deliberately creates novel challenges each year.
Winning a Gold medal as an AI system is the current biggest status prize for any AI company (Silver being still quite impressive), so we can assume that a few will attempt to face the challenge concurrently with the human contestants, maybe sharing their progress in real time to be the first ones to post their results.
For the results to be accurate, however, AI should not receive special treatment or modified problems – they should face the same six new problems created for IMO 2025 as human contestants, and tackle them in real-time. AI submissions should be assessed using identical marking criteria, creating a truly level playing field.
In all likelihood, however, we will not get that level of transparency from the contestants. The AIs might also need extra time, as humans only have 2 days to go through the six problems, and from what I understand, AI systems likely will not be able to match that speed.
The competition will reveal not just whether AI can solve the problems, but also how their approaches differ from human contestants. Will machines discover the same elegant solutions prized by humans, or will they find alternative paths that reveal new mathematical insights [this did not happen in 2024]? Or will they fail?
AI’s secret sauce: LEAN
Geometry problems aside, most AI teams working on IMOs have adopted Lean as part of their pipeline. Lean is a “programming” language that was invented at Microsoft Research in 2013 to make mathematical proofs and software systems 100% verifiable — not just believed to be correct, but proven correct with no ambiguity.
For mathematics, Lean allows you to write formal proofs that are checked line by line by a computer. This eliminates human error, scales to massive theorems, and creates a library of rigorously validated mathematics (mathlib).
As powerful as it is, Lean is also incredibly hard to learn and master, as has a very finite community of experts.
Why use Lean in the context of Large Language Models? What’s wrong with using natural language? It’s what you would use as a human to write your proofs, even as a professional mathematician (unless you are Pr. Kevin Buzzard from Imperial College and super ahead of your time).
Actually for training AI, natural language is terrible, as, contrary to very basic maths, where any random annotator can check the correctness of the proof, it’s incredibly hard to validate the outputs of your specialised LLM.
When the problem allows for very simple validation (for example, problems where the solution is “a number” that can be verified), these types of models can be trained. However, it does not cut it for the IMO.
That’s where Lean comes into play. Lean is a language that serves as an interactive theorem prover used to write and verify formal mathematical proofs. It ensures that every proof step follows strict logical rules, removing ambiguity and human error. Researchers use Lean to build a growing library of certified mathematics (mathlib) and to verify complex theorems.
Instead of using natural language, our AI teams first transcribe the problem in Lean, enabling the model to be trained with RL, such that the correctness of the proof can be verified at all times.
Every move can be checked automatically, so the AI can learn by trial and error without confusion. It also helps build clean training data, since all proofs in Lean are precise and unambiguous.
The most formidable barrier for AI in the IMO emerges when problems resist formalization in Lean. See that little first arrow (“IMO problem to Lean problem”)? It’s not a trivial arrow at all. Some IMO problems are very hard (impossible?) to formalize in Lean, making them therefore out of reach for most of the potential contenders, as it's the key component of their model.
Give me a second for an illustrative tangent. Let’s go back to the 1988 Australian IMO edition with our 12-year-old Terence Tao, who turned 13 on the day of the results and was carried on the shoulders of the other contenders as he left the room. Let’s look at the 6th problem, the one Terence did not manage to solve:
In 1988, 11 candidates managed to find a solution, including one Bulgarian boy, Emanouil Atanassov, who was awarded a unique special prize for the fact that his solution, written in Cyrillic, was perfect and about half a page in length.
To this day, despite the existence of a half-page solution, nobody has been able to formalize this problem in Lean.
Not Lean but: Geometry is done for
Geometry, however, has been tackled by AI researchers differently (despite the existence of LeanEuclid), as you have alternative Euclidean geometry solvers that can provide the ground truth for an RL-trained or neurosymbolic model, as demonstrated by the famous DeepMind paper Alphageometry (combines Gemini LLM + symbolic engine (DDAR) + tree-search for constructing auxiliary geometry - 2024). Meta and OpenAI also attempted to tackle the problem, with similar success.
We can safely assume that AI systems will be able to solve all future IMO geometry problems.
Possible Lineup
Disclaimer: This is a long list based on my own speculations of which teams could have the chops to go alongside the humans (and it’s not my place to disclose which team will definitely participate - if you know, you know). Please follow the different teams’ socials in the next few days, as there are very strong contenders for a silver or a gold medal, given the quality of their previous work.
Here is a long list of teams who could be in the lineup, and their latest IMO-related publications:
The Obligatory DeepMind
Pro: Feb 2025 – AlphaGeometry 2 achieves gold-medalist coverage on geometry: 88 % of IMO 2000-24 tasks. Core solver for DeepMind’s planned IMO-2025 run. arXiv
Pro: Jul 2024 – AlphaProof + AlphaGeometry 2 hit 28 / 42 points (4 / 6 problems) on IMO 2024—roughly a silver medal. Google DeepMind
Cons: none
Overselling-much OpenAI
Pro: Sep 2024 – IBL News independent test. o1 solved 83 % of an IMO qualifier, far above GPT-4o. IBL News
Cons: qualifier ≠ full IMO (qualifier problems have a “given” solution, like we discussed earlier, you can validate the results from the output, not from the proof so it’s much easier to train an AI system towards this)
Pro: Apr 2025 – “DeepSeek-Prover-V2” hits 88.9 % pass on MiniF2F and solves 6 / 15 recent AIME problems. Open-source Lean-4 prover built from DeepSeekMath-7B & 671 B checkpoints. arXiv + arXiv
Cons: … none, if IMOs are in their roadmap
Emergent Harmonic AI (start-up - 75M$ raised)
Pro: Jan 2025 – “Aristotle” pushes MiniF2F to ~90 % which is very impressive. Internal Lean RL prover; public post details dataset fixes and new NL interface. Harmonic Reality check: record is self-reported; full proofs not released.
Cons: might not be in line with their strategic goals to spend massive compute towards an academic challenge, they might skip it
Pro: Apr 2024 – TechCrunch. Startup pursues category-theoretic, memory-factored architecture to reach Olympiad-grade reasoning with smaller models. TechCrunch | Jun 2025 – website update claims internal IMO-geometry prototype under test symbolica.ai
Cons: Despite the likely neurosymbolic advantage when it comes to computational costs, can they hold their own against computational giants?
Greater Good Powered Numina (non-profit)
Pro: Aug 2024 – NuminaMath-7B-TIR wins AIMO Progress Prize 1 (29/50). Weights open-sourced. Hugging Face
Cons: Can a non-profit organisation match Deepmind and other big companies despite limited resources? I’d love to see them win!
What about anforeseen team from the AI community/academia (?)
Pro: Lots of positive results from independent teams on the intermediate AIMO challenge
Cons: you need a buttload of compute for the real thing so it’s unlikely an unfunded squad can take on the majors here
No Meta? Probably not. Despite excellent AI x Math researchers (like Fabian!), they have not been super active at least on the scientific publication space on that topic since 2022… but you never know!
Conclusion: def. more exciting than the Paris Olympics
As the competition approaches, several far-reaching implications come into focus, extending well beyond the mathematical domain.
The Compute Arms Race vs. Methodological Innovation The contest will likely reveal a fundamental tension in the development of AI reasoning. On one side stands the brute-force approach: throwing massive computational resources at the problem through the "O1/O3" style long chain-of-thought models and Monte Carlo Tree Search (MCTS). These approaches essentially use raw processing power guided by massive datasets to navigate complex reasoning chains. As one insider noted, most teams will deploy over 1000 GPUs (yes, you heard right), costing enormous sums to tackle these high school-level math problems, revealing just how computationally expensive true reasoning remains.
On the opposing side lies the potential for methodological breakthroughs – what several participants hope might emerge as "a totally different method." The competition could reveal whether simply scaling existing approaches is sufficient or if fundamental innovations in how machines conceptualize problems are necessary for higher-order reasoning.
Formalization as a Bottleneck A critical insight emerging from competition preparations is that most teams seem to be bypassing natural language in favor of formalizing problems directly in the Lean theorem prover. This approach offers decisive advantages for reinforcement learning since it provides unambiguous verification of correctness. However, it creates a significant bottleneck: the limited availability of Lean experts to formalize problems. As one insider shared, "the team that could hire the most annotators/Lean programmers is helped here as it's a very small community."
This dependency raises important questions about AI reasoning capabilities in domains where formal systems either don't exist or where formalization is prohibitively complex. Suppose the IMO competition demonstrates that the best-performing systems are those with the most comprehensive formalized datasets rather than the most sophisticated reasoning architecture. In that case, it suggests a path-dependent future where AI reasoning capabilities advance fastest in already formalized domains.
Perhaps most significantly, success at the IMO would indicate AI's capacity to meaningfully assist with theoretical mathematics research—the most distinctly human of intellectual pursuits.
Well, that’s all for today - see you fellow nerds soon.
Marie
P.S. I’m super keen to meet more people working on Math x AI. If that’s you, please reach out!
If you’d like to spend more time on this topic, you might enjoy…
AI for Mathematicians (Leo Dreyfus-Schmidt, 18 Apr 2025) Hands-on field-report: a working mathematician shows exactly which LLM + proof-assistant tricks shorten real research loops — and where they still fail.https://dsleo.github.io/
Can AI Do Maths Yet? (Xena Project, 22 Dec 2024) A formalist‐leaning mathematician audits the 2024-era models (o3, FrontierMath) and quantifies their 25 % success-rate, separating hype from reality.xenaproject.wordpress.com
“Solving Olympiad Geometry without Human Demonstrations” (Nature, 2024) Landmark paper behind AlphaGeometry: shows a neuro-symbolic solver matching human IMO gold-medalist level on Euclidean geometry, no handcrafted data.nature.com
“Mathematical Discoveries from Program Search with LLMs” (Nature, 2024) Introduces FunSearch—LLM-guided code evolution that discovers new theorems in combinatorics and computer science, hinting at AI as a creative collaborator.nature.com
FunSearch Blog Post (DeepMind, Dec 2023) Accessible explanation of FunSearch’s “LLM + evaluator” loop; clarifies why guarded evolutionary search beats raw text generation for math discovery.deepmind.google
AlphaGeometry Blog Post (DeepMind, Jan 2024) Breaks down the self-play pipeline that lets AI construct geometric proofs competitive with top Olympiad students—useful blueprint for other domains.deepmind.google
LLMs & Math: A Review of Approaches and Progress (Medium, Nov 2024) Quick survey of benchmarks, datasets, and open problems; good primer if you need the entire landscape in one sitting.Medium
Amazon Science – Automated Reasoning Research Area (living page) Shows how industrial-scale formal methods (sat-solving, model-checking) underpin AWS security and may scaffold future math-capable LLMs.Amazon Science
Amazon Scholar Solves Century-Old Problem (blog, 3 Apr 2024) Case study: automated SAT infrastructure cracks a long-open combinatorial puzzle, demonstrating practical impact beyond toy benchmarks.Amazon Science
How the Lean Language Brings Math to Coding (Amazon, 16 Aug 2024) Explains why Lean is fast becoming the lingua franca for formal proofs and how it interfaces with AI systems like AlphaProof.Amazon Science
Solomonic Learning: LLMs and the Art of Induction (Amazon, 18 Nov 2024) Thought piece arguing future models must juggle memorization, computation, and logical induction—useful mental model for evaluating new architectures.Amazon Science
AlphaProof (DeepMind, Jul 2024) Reinforcement-learned prover that, together with AlphaGeometry 2, reached IMO silver-medal level—proof that language-model reasoning scales with self-play.deepmind.googleThe Guardian
Training Data Podcast – Misha Laskin (Sequoia Capital, 2025) 45-minute audio on what AlphaGo’s self-play lessons mean for agentic LLMs; worth it if you invest in AI infrastructure or research scaling laws.sequoiacap.com
